I Tried To Understand How Computers Work and Instead I Understood the Universe (Part 1 - Electricity)

Thinking about electricity

The Innocent Beginning

Computers store "data" (Whatever the hell "data" is) as binary 1s and 0s, fair enough

Computers transmit binary by encoding binary data as voltages, which is then decoded to binary, okay

Computers use binary because it maps to logical operations, but also because more voltage levels (to represent more states) increases the sensitivity of encoding/decoding, more errors

??? There is a limit to how much data can be transmitted in a given space because something, something, electricity stuff ???

And, if I'm being honest with myself, I didn't really understand the "encoding binary data as voltages" bit earlier either

In the first place, what exactly is a voltage? (Other than a line that sometimes goes up and sometimes goes down)

Voltage

Difference of electrical potential energy per unit of charge between two points

...Wtf? Let's start from the beginning, with what the hell electricity is in the first place

Electromagnetic Force

One of four fundamental forces (So don't think too much about why it exists, take it as a given)

(I'm also only going to talk about particles in a vacuum to keep the explanation simple. Once we start talking about bigger things, it's easy to become confused by inaccurate comparisons)

Forces are properties of particles (Or, more accurately, interactions between particles. But I'm just going to use the former understanding because it's easier to reason about)

Forces "push" or "pull" other particles

For electromagnetic force, like attracts, unlike repulses, you already know this (If we have two particles of unlike charge, both particles are independently applying force on the other particle, it's not one weird "force" pulling both together. A metaphor might be two cars driving towards each other)

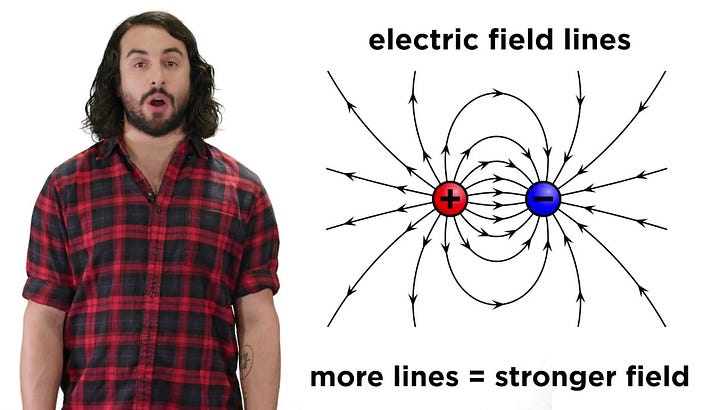
Electric Charges and Electric Fields

Professor Dave Explains, Electric Charges and Electric Fields -

Physics Made Easy, What is an Electric Field? -

Electrons are particles with negative charge, where charge is the property of attracting unlike and repulsing like (Electrons are not the only particles with negative charge, but those are beyond me)

Charges are quantised - Each electron has the same quantity of negative charge, and each proton has the same quantity of positive charge

An electric field is a region of space for which a particle with electric charge experiences electromagnetic force (Implicitly applied by another particle with electric charge)

A field is a region of space for which each point is associated with a quantity. Imagine an object placed on a grid, and all the cells of the grid have a number depending on the closeness of the cell to the object (An electric field has infinite range, but the quantity of force drops off quickly to very, very tiny amounts)

(The concept of a field is weeeirddd. I'm used to the physics of things colliding into other things, forces applied by "touch". A hurricane might blow something away at an apparent distance, but we know air is actually hitting the object being blown away. But electromagnetic force being applied at a distance is just another one of those take it as given things)

(We'll save the "magnetic" part of electromagnetic force for later, it's not needed to understand voltage)

Electric Potential (Energy)

Okay, we can finally get to understanding electric potential...

...Wait, what is energy?

Energy

Sabine Hossenfelder, What is Energy? Is Energy Conserved? -

Some definitions state energy is the capacity to do work, and work is energy transfer, which is annoyingly circular

The proper definition of energy is: The quantity conserved in a system with time-translation invariance

Time-translation invariance in a system just means a system whose equations do not change with time (This does not mean system does not change, since solutions the the equations can still change)

All of which is a long way of saying, energy is conserved, only where the energy is changes (With an asterisk for general relativity, but that's not relevant)

So we have a set of equations which describes a constant quantity of something, which we call energy (As a metaphor, we could observe two flasks connected by a tube. The system is filled with some amount of water, and we could describe this system with a set of equations. Energy is not a made up thing to balance the equations, we made up the equations to fit our observations of the system)

If we push two electrons together, the energy used to push them together is converted to potential energy (electrostatic energy)

If we stop pushing, the potential energy is converted to kinetic energy

Total energy is conserved at both steps

If we take the conservation of energy as an axiom, then potential energy must exist. (Which is something I've always struggled with, since potential energy is something which by definition I can't see, and how can something I can't see exist? But we could extend the flask metaphor from before, and hide the volume of water in one flask with black tape. Even though I cannot see how much water is in the blacked-out flask, knowing that the volume of water must remain the same within the system, and knowing the volume of water in the clear glass, I can derive the volume of water in the blacked-out flask)

So, my informal understanding of energy is:

• Energy must be conserved as an axiom

• Energy is either in moving particles, or in non-moving particles

• Note that it's not energy which moves particles, but forces (by pushing or pulling  particles)

• (Force is another incredibly weird concept they "teach" you about in high school but never properly explain. It's weird because we know energy must be conserved, and cannot be created or destroyed. But force seems to "create" energy out of nowhere. If we pop a new electron into existence next to an existing electron, the new electron is repulsed, but where did the kinetic energy of the repulsion come from? The problem with that thought experiment probably comes from popping a new electron into existence)

• If we instantiate a new tiny universe with a billion electrons in a tinier cluster in the universe, pausing time so they don't move, we observe that each electron has its own electric field, and therefore each electron has forces applied on it from the other electrons. The system has potential energy from the positioning of the electrons. Unpause time. Potential energy is converted to kinetic energy as the electrons repulse each other

• This thought experiment tells us that energy is, in some sense, a descriptor of the positioning of particles. And when we state work = energy transfer = force * displacement, we are just stating simply that the position of a particle which has energy transferred to it has changed (We need the force part of the equation because the force a particle applies is stronger or weaker depending on distance, so displacement by itself doesn't quite capture what positioning is)

(The understanding of energy as positioning clears up a confusion I've always had. How can a table with an apple on it not expend any energy holding up the apple against gravity? We need energy to resist forces, right? But, one, "We need energy to resist forces" is a misunderstanding based on the fact that "I, as a human, feel tired while holding up an apple against gravity, and I call feeling tired 'lacking energy'." And, two, the positioning of the apple has not changed)

Electric Potential

Physics Made Easy, What is an Electric Potential? -

Okay, now we can finally talk about electric potential

Electric potential energy is just the (not yet realised) tendency of an electron (or other particles with electric charge) to move in a certain direction because of its positioning relative to another particle with electric charge

We focus on electrons because the other common particle with electric charge, the proton, has a stronger force (appropriately named the strong force) applied to it, holding the atom together, so the proton doesn't move when we apply (a small) electromagnetic force to it

But aren't atoms also held together by electromagnetic force? Why doesn't the while atom move?

I'm guessing certain configurations of relative positions are stronger than others, and conductors are conductors precisely because they have electrons in a configuration which are less stable (free electrons)

(I don't really understand why "full valence shells" are more stable, so I'll just handwave away the particulars. It's sufficient for my purposes to understand that there are more or less stable configurations)

Put an electron down on an imaginary flat grid, and fill in the cells of the grid with a number representing how much energy a second electron would have if placed in that cell, with closer cells having more energy

If I put an electron down in a cell labelled e.g. 10 Joules (Big number for ease of reasoning, obviously it's going to be much smaller in reality). There is now 10 Joules of potential energy in the system (Ignore interactions for simplicity)

Put another electron down in the same cell. There is now 20 Joules of potential energy in the system

So the number we wrote in the cell really represents energy per electron. Or, more accurately, energy per quantity of electric charge of an electron

This is our definition of voltage (energy per unit charge), and almost our definition of a Volt (Joules per unit Coulomb of charge)

We can think of a Coulomb of charge as the charge of an arbitrarily large number of electrons. Arbitrary, because it was chosen to make other SI units play nice with it, and also because the Coulomb was defined before electrons were discovered

Voltage Two, Electric Bugaloo

The Science Asylum, Does Electricity Really Flow? -

Okay, so I now understand what a voltage is at a physics-y, conceptual-ish level

But how exactly does voltage work in a circuit?

If I connect one end of a wire to itself, there is no electricity "flow"

One, because the negatively charged electrons are attracted to the positively charged protons (And vice versa, but the protons are held in place by strong force, so only the electrons move) in the atoms of the metal in the wire

Two, because the free electrons in the wire are positioned "randomly" relative to each other, the repulsion forces applied between these free electrons is also "random"

So free electrons are moving around in a wire, just not in a pattern we would describe as a "flow", or movement in one direction

There needs to be some impetus to move the free electrons in one direction, with enough force, and the impetus in a circuit is a battery

I don't really care about the complicated chemical stuff at the moment, so I'm just going to say batteries are just two boxes in a bigger box

One box (anode) is filled with negatively charged atoms (negative ions), the other box (cathode) is filled with positively charged atoms (positive ions)

Negatively charged atoms just mean there are more electrons in the "orbit" of a nuclei than protons in the same nuclei. (By "orbit", I mean the electrons are more attracted to this particular nuclei than some other nuclei based on the electrons' current positioning)

The protons still attract the electrons but, intuitively, since there are more electrons than protons, it's easier to be repulsed than attracted, so electrons have a greater tendency to fly out of orbit

(Since we're talking about materials and not hypothetical particles in a vacuum, we need to remember that the atoms are surrounded by other atoms, so electrons flying out of orbit just fly into the orbits of other atoms. This was something I had a lot of trouble with since I kept implicitly thinking about particles in a vacuum)

(What happens at the edges, where the surface of the the conductor interfaces with air? A few electrons probably do fly off, but the angle of flight probably tends to be horizontal-ish due to the attraction of protons)

In the anode (and the metal conductor connected to the anode), free electrons are moving around randomly between the negative ions

Once a wire (with neutral charge), is connected to the anode, there are way more free electrons and repulsive force on the battery side, so tend electrons tend to move into the wire ("Electricity follows the path of least resistance" is just a confusing metaphor for this tendency. If a particle is being pushed more on one side than the other, obviously it moves in the direction of the stronger push)

(Also note that the equalisation doesn't happen instantaneously. Just because there is more repulsive force on side A in general, doesn't mean there aren't localised pockets where there is more repulsive force on side B)

There is a flow of free electrons from the anode into the wire until the electrons are equally spaced out in both materials, at which point we go back to the original scenario where free electrons are moving around randomly

The same equalisation between the anode + wire and the cathode if we connect the other end of the wire to the cathode

(Connecting a battery to itself is called creating a "short-circuit", because without a resistor to slow the flow of electrons, free electrons will equalise more quickly between the anode and cathode, more quickly depleting the battery)

(I kind of dislike calling it that, because, to my non-engineer mind, "short-circuit" = electronics breaking = bad. Then my brain conflates "this isn't what I want to happen bad" with "this is impossible bad" and I get incredibly confused. But what happens when we connect a battery to itself is exactly what we would expect to happen)

Okay, I think we understand enough to add a resistor to the circuit (I don't want to bother with understanding the mechanics of a lightbulb)

How resistors work is they are made of materials with atoms that are more irregularly packed, have less free electrons etc., so that when the free electrons from the wire encounter the resistor, there's a greater chance of collision with the atoms of the resistor.

The collisions vibrate the atoms, which eventually vibrate the atoms in air. These vibrations we call "heat"

The difficulty I have with resistors is that I keep thinking they work something like:

The electrons are speeding along until they unwittingly slam into the resistor. The free electrons, having lost some kinetic energy from the collision, limp across the rest of the circuit. So there is a difference in speed before and after the resistor

But we know that description is wrong, because the speed of electrons in a circuit is constant. The resistor slows down the overall speed of the entire circuit.

But how do I make that make sense? (Without referring to water analogies, where it doesn't make sense to me either, lol)

After thinking about it for a while, I think my problem was that I was thinking about single electrons. What probably happens is that some free electrons make it through the resistor, and some free electrons get repulsed back, backing up into the free electrons before the resistor, causing those free electrons to back up and so on. With the overall effect of equilibrating speed

Also of note is that current is the flow of charge across a "point" (Does the circumference of the wire matter?) per unit time, not the flow of electrons Electrons only flow a few centimetres an hour (drift velocity), but electrical appliances turn on and off immediately

What happens is that as soon as the first electron moves a little, it's electric field also moves (at the speed of light)

The field applies a force on other electrons in the wire, so the electrons move slowly, but the motion of all electrons happens at once