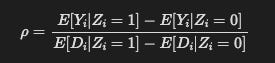Notes on Instrumental Variables

Also a review of statistics in general

Review

Statistics

• All statistics is the study of group averages (Probability is in the Mind, "God does not play dice with the universe")

• Individual (True causation, effect on individual) -> Group (Average effect on individuals within group) -> Observation of group (Omitted Variable Bias)

Purposes of Statistics

• Description (Policing vs Crime)

• Prediction ("If nothing changes", Stationarity)

• Causation ("What happens if I press the red button?")

  • Paul Holland - "No causation without manipulation"

Why is linear regression reasonable?

• The best predictor of Y is E[Y|X], or the Conditional Expectation of Y

• Linear regression is an estimate of E[Y|X]

• Therefore linear regression is a good predictor of Y

RCTs

• But E[Y|X] does not generally have a causal interpretation, unless all causal paths have been account for

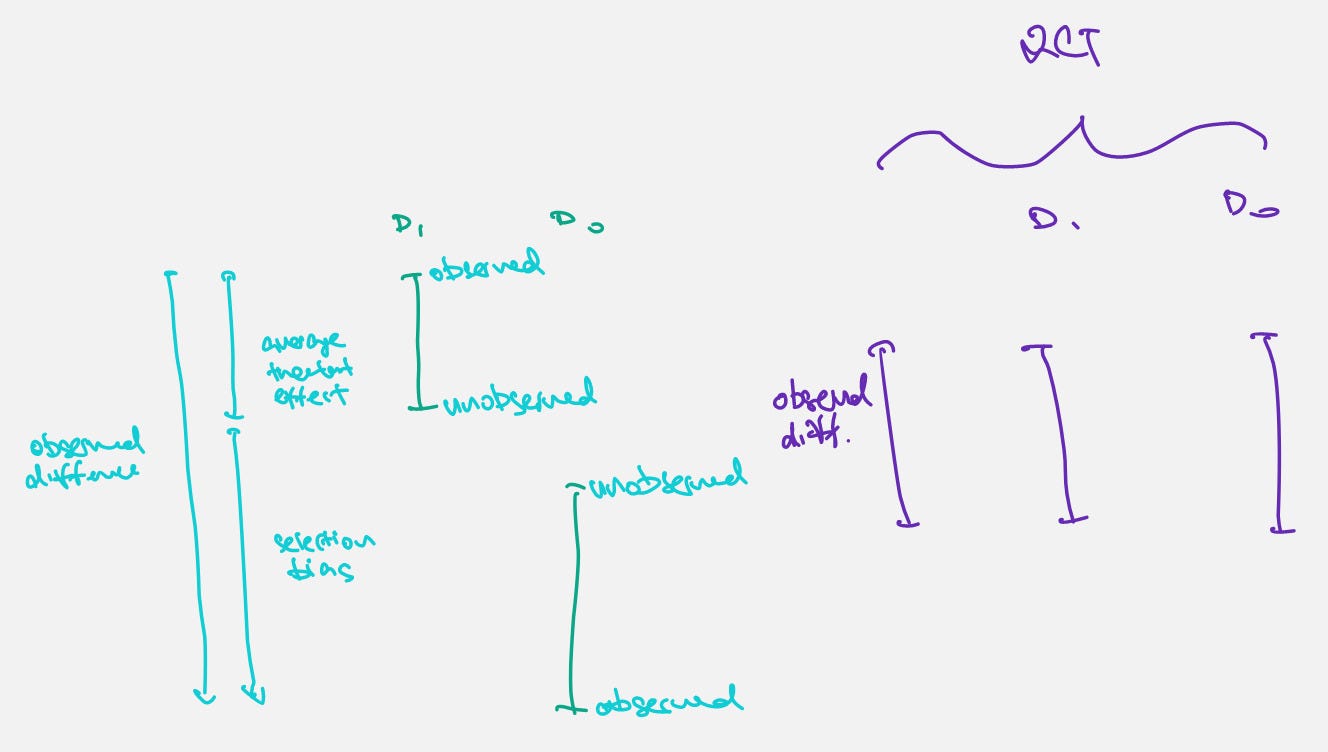
  • No omitted variable bias (of which selection bias is a subset)

  • No endogeneity (i.e. we have exogeneity, or equivalently E[ε|X] = 0 (Zero Conditional Mean, note that if this is true, E[ε] = 0 and cov(X, ε) = 0))

• RCTs remove omitted variable bias by controlling for relevant variables during assignment
  - Controls must be upstream of assignment (or there would be no point in assignment, lol)
  - OVB is still possible if the wrong things are controlled for
  - Does not handle simultaneity (But what does? 🤔 Systems thinking?)
  - OVB is not the only source of error e.g. measurement error

A much clear picture of what's happening with the Potential Outcomes Framework than some stupid equations

IVs

• Not always possible/preferable to conduct RCTs (cost per unit reduction of uncertainty)

• Angrist (Mostly Harmless Econometrics, C4) - "Like most people who work with data for a living, we believe that correlation can sometimes provide evidence of causal relation"

• Given: Random assignment (Intention to treat) -> Treatment (Non-random selection) -> Observed effect

• A on B * B on C = Observed A on C

• A on B is known (from random assignment), B on C is unknown, A on C (Reduced form) is observed

• B on C = A on C / A on B

• With proper notation (there should be hats, but I can't be bothered, lol):

  • Y_i = α + ρ * D_i + η_i (Y is outcome, D is treatment)

  • D_i = π_0 + π_1 * Z_i + u_i (Z is instrument)

  • ρ = cov(Z, Y)/cov(Z, D)

• If Z is binary (Wald test):

  

• Conditions:

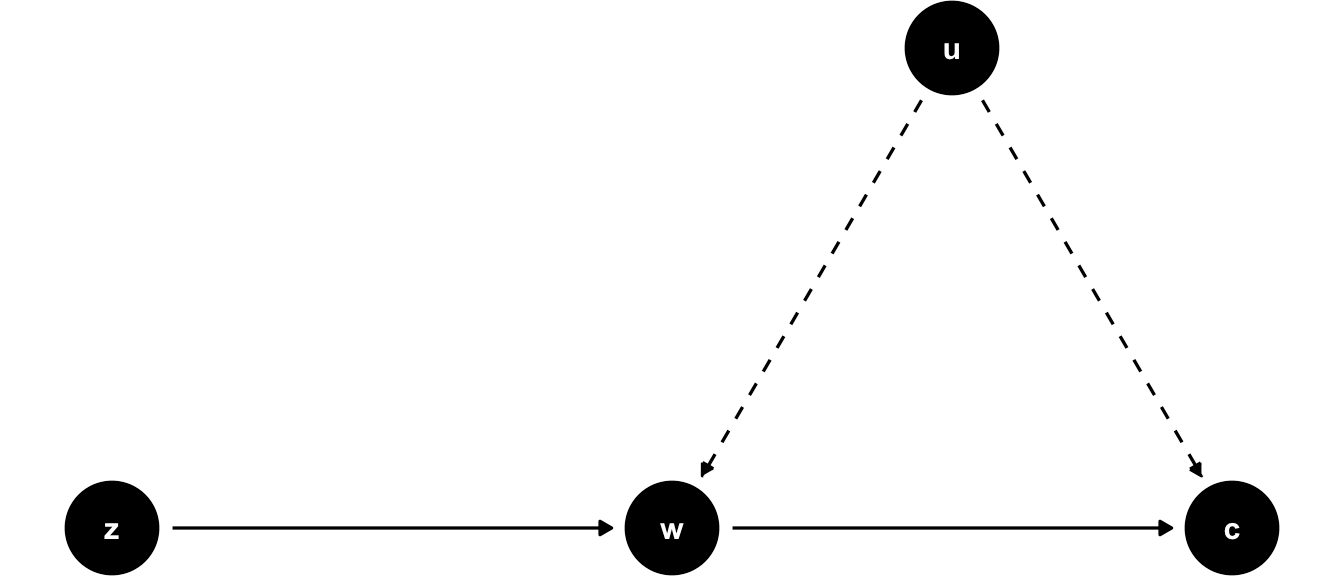
  • Non-zero (Preferably large) first stage effect (Relevance/Inclusion)

    • E[D_i|Z_i = 1] != E[D_i|Z_i = 0]

  • Independence (Random assignment is random)

    • E[η_i|Z_i = 1] != E[η_i|Z_i = 0]

  • Exclusion (No alternate causal paths i.e. random assignment has no direct effect on observed outcome)

  • Monotonicity (If heterogenous effects, i.e. Different people have different Intention to treat -> Treatment responses, No contrarians who treat ONLY if not assigned to treat) ??? Not sure why this is an important condition

Something something LATE theorem

IV Diagrams

Source: ScPoEconometrics

Source: Introduction to Instrumental Variables