This is going to be a rant, but I think it's an important rant, which goes at the heart of what I find most frustrating about learning technical subjects: How it is taught. For example, if you've ever had a statistics class, you might have seen this equation:
And you might know that it is called a "linear regression". You might even know that it works because it "minimises the sum of squared errors". Now I ask you, why does it work? The standard explanation is: We want to minimise error to get the best fit; We need a positive error to minimise; Squaring the errors makes them positive, weights extreme errors more heavily, and has some nice mathematical properties. Wanting to minimise error and needing a positive error I won't complain about, since there's no other reasonable definition of "best fit". But weighing extreme errors more heavily and having nice mathematical properties - These seem like choices, and these choices never seem to be justified, only assumed.
When I was in school, when something like that was taught to me in class, I immediately stopped paying attention to anything else. Wasn't that what I was supposed to do as a serious student™? To not memorise what was taught and instead understand the material deeply? Logically, if the premises are false, the conclusions based on those premises must also be false. Who cares if minimising the sum of squared errors has nice mathematical properties, if it's the wrong thing to do? So the very first step of learning something must be to firmly establish its premises, and if those premises weren't established, everything else was pointless.
As you might expect, I got very, very stuck on most topics. And when I wasn't stuck, when I gave up and "just memorised" certain rules, I always felt deeply dissatisfied. I hated "studying" in this way, and so I often didn't.
The problem with teaching linear regression - or any other technical topic - this way is that it's backwards. The equation is placed first, and then it is explained, as if the equation was carved from physical laws. It is not. What always fails to be said is that the equation is just formality. If you threw me a scatterplot and asked me to produce a line of best fit, I would very intuitively draw a line trying to "balance" the points around the line, probably prioritising the "balance" of extreme points over central points because they're more visually obvious. But it's a hassle to do this for very large data sets or for multiple data sets. So I want to find some pattern in what I'm already doing, and from this pattern define an equation or procedure that a computer can calculate or follow.
I map the steps of what I'm doing to the steps of "linear regression": Balancing the points can be done by minimising the sum of errors; Prioritising extreme points can be done by squaring the errors. Linear regression is nothing more than a tool which happens to have the properties that I want, in the same a way a kitchen knife is nothing more than a tool which happens to have the properties I want (hardness, sharpness, convenient hand-shaped handle) when I want to cut a tomato.
This seems obvious when stated plainly, and any reasonable teacher would agree that the things they teach are just tools. But knowing that something is true and acting as if it is true are two different things: When the slides are a wall of unfamiliar Greek; When there's no description of how we would solve the problem without the math; When there's no description of the problem's features, and which math objects have those features; When students confuse the method and the math which describes it; When students imagine a line drawn by the equation is somehow more correct than a line drawn by hand; When students are afraid of "linear regression" or "time series" in a way they would not "kitchen knife" - It's obvious that these tools are not being taught as secular tools, but as sacred objects beyond mortal understanding.
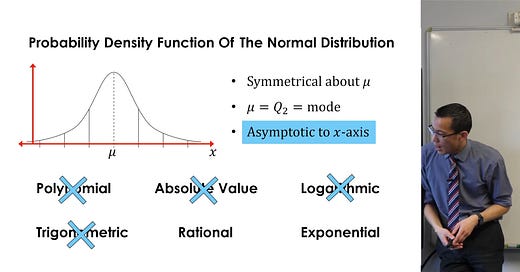
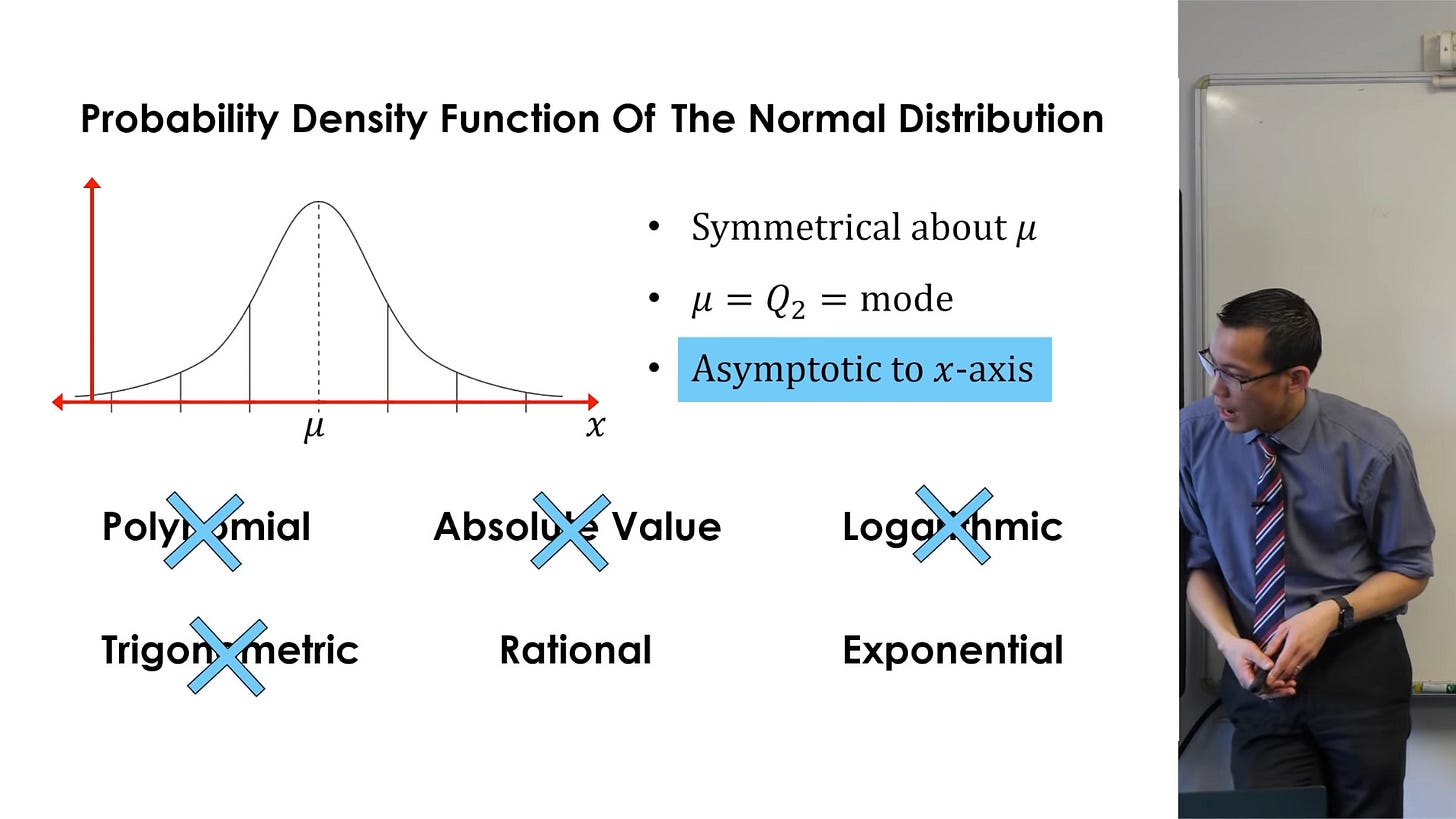
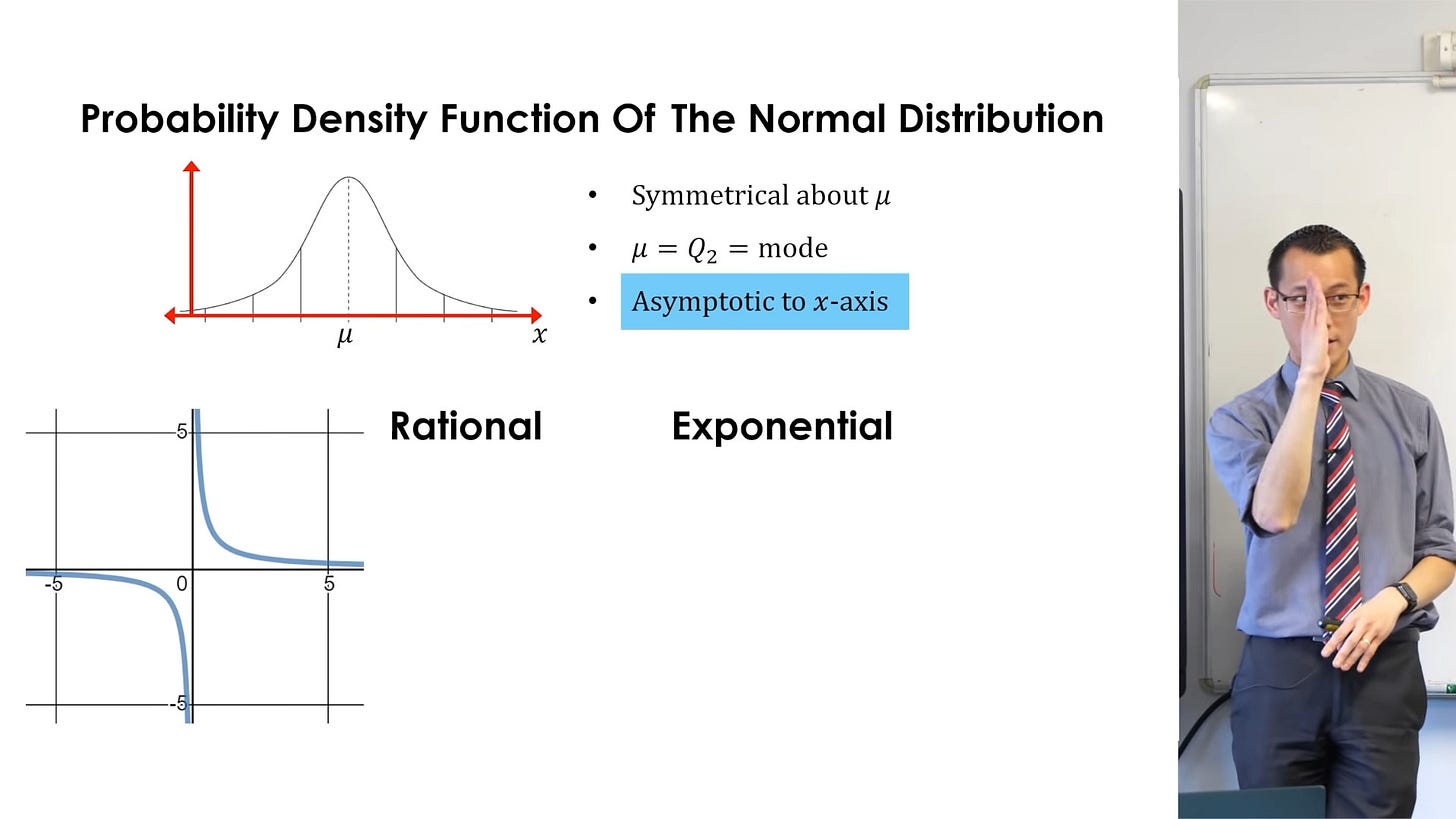
What would be a more "tool-like" way of teaching? Consider the following derivation of the normal distribution, given by Eddie Woo, where we start from a function which has the asymptotic property, and build up to have the required properties of a normal distribution:
A linear regression is just when there appears to be a trend in the data, and I want to describe that trend. A time series is when there appears to be a trend in the data, but also some repeating pattern. I can therefore do a linear regression of some vaguely repeating data to get the trend, then remove the trend from the data to get the repeating pattern. Formally defining this method can be done in various ways, just as we can have various kitchen knives. There isn't really a "best" kitchen knife, and like me you probably use the "standard" kitchen knife for everything. And terrifying ourselves by imagining a kitchen knife is more complicated than it really is will just make us act like a teenager who is afraid of the kitchen because they were taught knives are ~dangerous~ as a child.
Learning that "math" is really just a collection of objects, each with their own properties that may or may not make them useful as tools, instead of some mysterious "fabric of the universe" is what made math make sense to me. The imaginary number i is not sqrt(-1), woven into the fabric of the universe for inexplicable reasons. It's a + shaped object where if I color the right point red and performed a certain operation on it, the + shaped object rotates so that the red point is now on top. I arbitrarily label the right position 1, the top position i, and the operation *i. And I define the operation *i to return the red point to its original position in four steps: 1, i, -1, -i, 1. This is why Euler's formula:
makes sense.
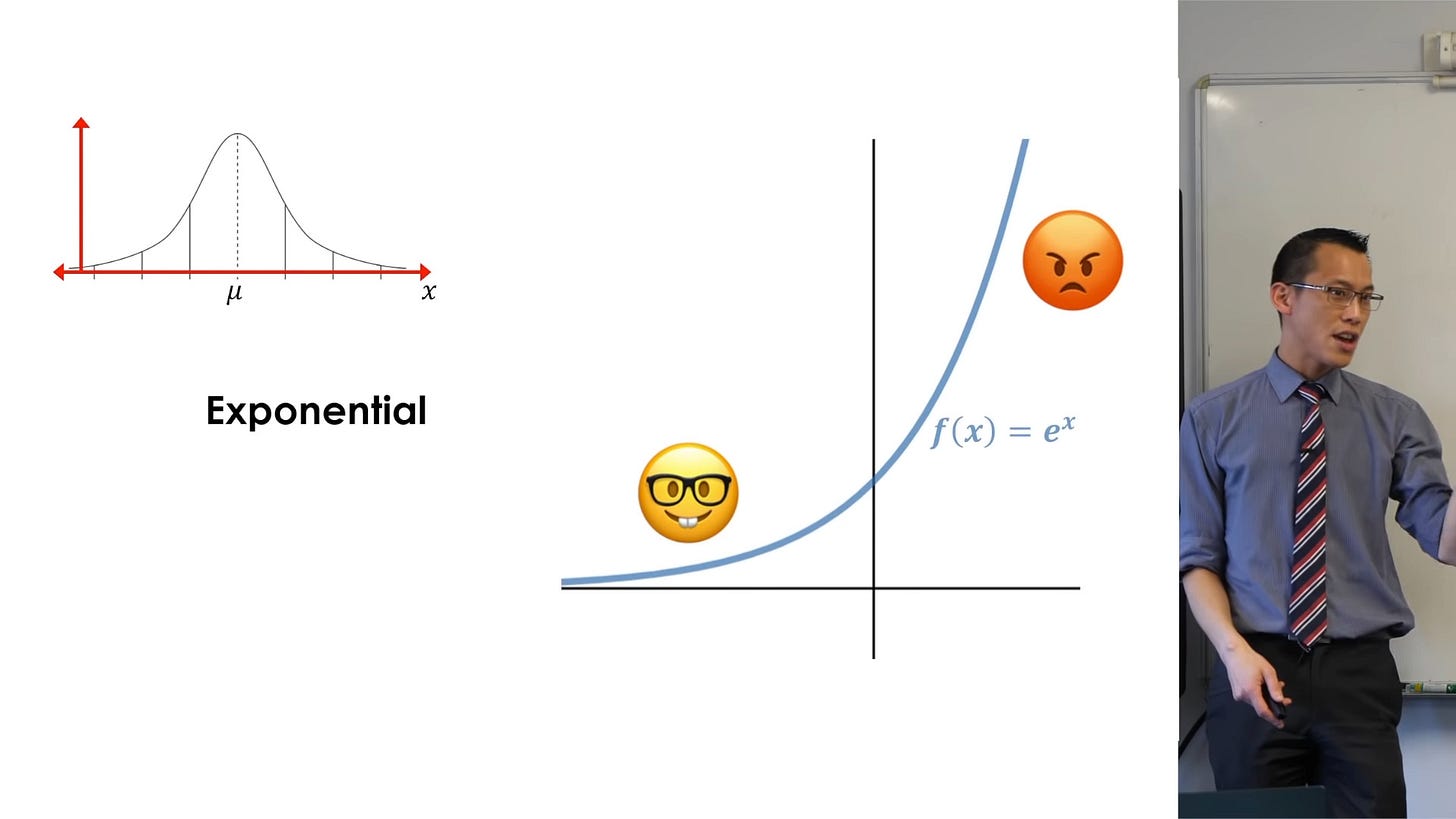
The exponential function e has property of returning to its original position in one step under differentiation:
While the cos and sin functions have the property of returning to its original position in four steps under differentiation:
It makes sense to add i somewhere in e to make the number of steps match between the exponential function and the sine functions - in the same way we might put a vertical gear and a horizontal gear together if we want to make a gatcha machine have a vertical turning thing to deposit a coin but a horizontal turning thing to drop the prize - even if it takes some trial and error to construct the correct equation/arrangement of tools.
We use e in electrical engineering to describe AC currents because AC currents are by definition sinusoidal, and because differential equations - which describe the present state as the consequence of past states and some fixed rate of change - have the property of "self-similarity" under differentiation. e has both required properties.
Similarly, the labels 1, 2, 3, 4, … are just labels we stick onto an infinitely long, segmented object. We could just as easily label each segment as a, b, c, d, e, … using other symbols when we run out of alphabets. It's much harder to work with because we're not used to the new labels, but the choice of labels is just convention.
Fundamentally, the world is this gross, messy blob of complicated things, and we have accumulated some tools to make tiny parts of the blob more regular and easier to work with. Wrongly assuming that these tools can be used on the whole blob either 1) makes us use these tools in places where they don't work, or 2) get really confused and waste time trying to figure out what went wrong when we think they "should" work, but they clearly don't???






a couple of points
One of the important insights about linear regression and the reason why one *should* look at the sum of squares formula that the linear fit by minimizing squared errors usually does not match the intuitive "trendline". If a statistically uninformed student is asked to draw a trendline in a scatterplot, they trend draw line balanced in the middle of the "mass" of the points in scatterplot, which actually looks like more an errors-in-variables trendline [1] than the classic linear regression. The linear regression minimizes errors only in the Y axis.
(Now there is an extremely good question why the classic linear regression choices to do it, which is rarely both asked and answered.)
Likewise, the "tool-like" teaching of normal distribution sounds slightly backwards to me. Definition of 'asymptotic' is a non-trivial thing. And in the 4th step, why would we be worried about "peak" in exp(-|x|)? It was the distribution Laplace obtained while trying to find an error model (before he found central limit theorem). Laplace might have stopped there if it matched the real phenomena. So we should ask: why is the normal distribution, with its bell-like curve, a useful tool? Because of the following mathematical fact (generalization of the central limit theorem): if you have a random variable Y that is a sum of independent random variables X_1, ... X_n with constant variance, Y will have a normal distribution when n is sufficiently large. And many real life phenomena that a statistician will measure are (sort of) measurements of sum of independent random variables.
Proof-based courses try to teach these kind of things, but unfortunately even proof-based courses often merely present the proof and maybe references for it. Very rarely is presented the history of scientific discussion / arguments that lead to the proofs presented in the textbook.
[1] https://en.wikipedia.org/wiki/Errors-in-variables_models
On second thought, if I said it on Reddit I should say it here too.
I work as a math tutor. Part of me agrees very strongly, while another part thinks this is all nonsense.
I know that that's a weird reaction, so I'll try and untangle it.
It is indeed much better to understand math as a collection of tools. I often try to help students see things that way. Many students really do need explanations like these, and I like the choice of examples.
But the thing is, our system demands a certain level of "mechanical" ability at each grade level. For example, we expect elementary school children to handle fractions and long division. And the underlying logic there is often way beyond (https://www.smbc-comics.com/comic/2014-12-06) the ability of the children to understand. Many children won't even follow age-appropriate explanations. Sometimes because they lack the talent, but more often because they lack the interest.
Whenever the "right" approach fails - and it fails a lot - you can only resort to teaching math like a magic spell. Follow the rules, get the result. Under time pressure, and/or with a large class, you may need to lead with that. And unfortunately that kind of teaching makes it difficult to view math in that flexible tool-oriented way.
There is a silver lining. The ability to simply execute instructions mindlessly (even when you have no idea why they've been given to you) is very useful in math. And in life. You gotta have that part that questions things, but it also helps if you can turn it off.
PS: I actually think it would benefit many struggling math students to read essays like this one. Might give them some insight into how it feels to actually be good at the subject, even if they don't follow the examples at all.